Paper Title
DeepWave: A Recurrent Neural-Network for Real-Time Imaging
Matthieu Simeoni, Sepand Kashani, Paul Hurley and Martin Vetterli
In Neural Information Processing Systems (NeurIPS), 2019
acoustic imaging
title={Deepwave: a recurrent neural-network for real-time acoustic imaging},
author={Simeoni, Matthieu and Kashani, Sepand and Hurley, Paul and Vetterli, Martin},
journal={Advances In Neural Information Processing Systems},
year={2019},
volume={32},
}
TL;DR: This paper proposes a lightweight RNN to reconstruct spherical acoustic maps in real-time. The network is based on LISTA and it is trained with proximal gradient descent.
1. Introduction
Previous work: Delay-And-Sum (DAS) beamformer [1, Chapter 5]. Idea: Real-time reconstruction of acoustic spherical maps based on LISTA [2]. Limitations: It can reconstruct only high resolution microphone arrays
2. Background
2.1 Steering Matrix
The steering matrix is a matrix that contains the steering vectors of the microphone array. The steering vector is a vector that contains the phase shifts of the microphones in the array.
Signals can arrive to the microphones from different positions and angles. A direction can be parametrized as:
- Azimuth \(\theta\): The horizontal angle of arrival.
- Elevation \(\phi\): The vertical angle of arrival.
- \( k = \frac{2 \pi}{\lambda} \) is the wavenumber.
- \( d \) is the distance between the microphones.
- \( \lambda \) is the wavelength.
3. Proximal Gradient Descent
DeepWave reconstructs the images with a Recurrent Neural Network trained with Proximal Gradient Descent (PGD) by optimizing: \[ \hat{x} = \arg \min_{\mathbf{x} \in \mathbb{R}^{N}_{+}} \frac{1}{2} \| \hat{\Sigma} - \mathbf{A} \, \text{diag}(\mathbf{x}) \, \mathbf{A} ^ H \|^2_F \quad + \quad \lambda \left[ \gamma \| \mathbf{x} \|_1 + (1 - \gamma) \| \mathbf{x}\|_2^2 \right], \label{eq:objective-function} \tag{Eq. 3} \] which, after vectorization becomes: \[ \hat{x} = \arg \min_{x \in \mathbb{R}^{N}_{+}} \frac{1}{2} \| \text{vec} (\hat{\Sigma}) - (\overline{\mathbf{A} } \, \circ \mathbf{A} ) \, \|^2_F \quad + \quad \lambda \left[ \gamma \| \mathbf{x}\|_1 + (1 - \gamma) \| \mathbf{x}\|_2^2 \right], \label{eq:objective-function-vectorized} \tag{Eq. 4} \] where:
- \( \hat{x} \) is variable being optimized..
- \( \hat{\Sigma} \) is the estimated covariance matrix.
- \( \boldsymbol{A} \in \mathbb{C}^{M \times N} \) is the steering matrix.
- \( \boldsymbol{A} ^ H \) is the Hermitian of the steering matrix.
- \( \text{diag}(x) \) is a diagonal matrix with the elements of \( x \).
- \( \lambda \) is the regularization parameter.
- \( \gamma \) is the regularization parameter, the trade-off parameter between the \( \ell_1 \) and \( \ell_2 \) norms.
- \( \overline{\boldsymbol{A} } \) is the conjugate of the steering matrix.
- \( \circ \) is the Hadamard product.
- \( \| \cdot \|_F \): The Frobenius norm, which measures the difference between the target matrix and the approximation.
4. Methods
Given the covariance matrix \( \hat{\Sigma} \in \mathbb{C}^{M \times M} \), where \( M \) is the number of microphones, the network reconstructs the spherical acoustic map (SAM) with 2 layers. \( \mathbf{x} \) denotes the neuron at layer \( l \) in Eq. 6 and Fig. 1.
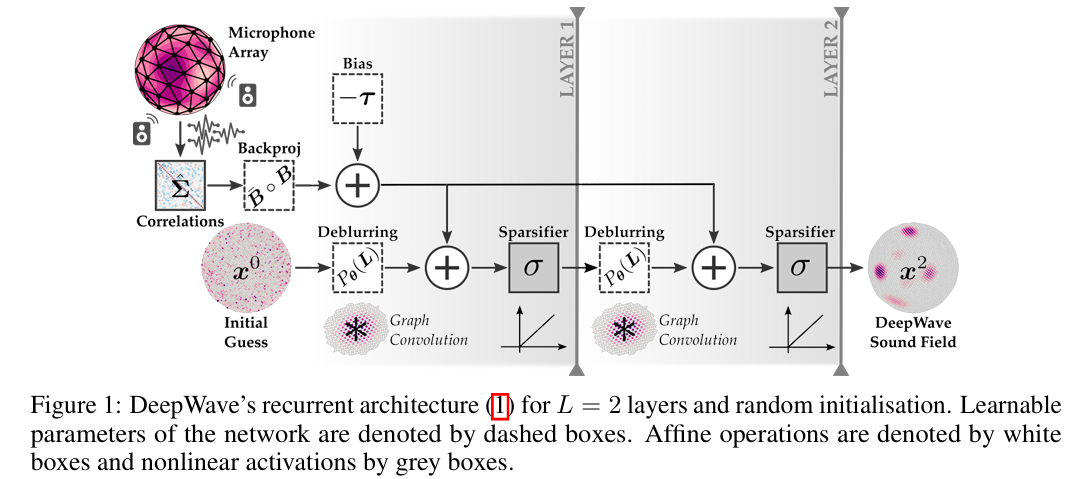
Fig. 1. DeepWave's network.
- \( \mathbf{x}^{l} \) is the neuron at layer \( l \).
- \( \sigma \) is the ReLU activation function.
- \( P_\theta \) is the deblurring operator and \( P_\theta (\mathbf{L}) \) the deblurring matrix.
- \( \mathbf{L} \in \mathbb{R}^{N\times N} \) is the graph Laplacian.
- \( \mathbf{\hat{B}} \) is the conjugate of the steering matrix.
- \( \mathbf{B} \) is the steering matrix.
- \( \tau \) is the threshold.
- \( \hat{\Sigma} \) is the estimated covariance matrix.
-
\( \mathrm{vec}(\cdot) \) is the vectorization operation.
Let \( \mathbf{A} \in \mathbb{C}^{M \times N} \) be a matrix, where \( M \) is the number of rows and \( N \) is the number of columns. The vectorization operator \( \mathrm{vec}(\cdot) \) reshapes the matrix \( \mathbf{A} \) into a vector of dimension \( M \ N \times 1 \) by stacking its columns: \( \mathrm{vec}(A) \in \mathbb{C}^{M \ N \times 1} \). The operation is defined as: \[ [\mathrm{vec}(\mathbf{A})]{M(j-1)+i} = [\mathbf{A}]{ij} \quad \mathrm{for} \quad i = 1, \ldots, M \mathrm{ \quad and \quad } j = 1, \ldots, N \label{eq:vectorization} \tag{Eq. 7} \]
© Copyright © All rights reserved | Carlos Hernández Oliván | Colorlib